Notes on single particle motion I

Charged particle motion

\[m\frac{d \bm v}{dt} = \pm q(\bm E + \bm v \times \bm B)\]

$m$: particle mass; $q$: (unsigned) particle charge
If fields are stationary, mechanical energy is conserved
Other exact conservation laws may exist in each problem

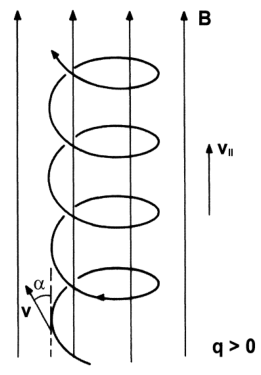
Constant and uniform $\bm B$ field

Take $\bm B = B \bm 1_z$:

$\frac{d v_x}{dt} = \pm \frac{qB}{m}v_y;$ $\frac{d v_y}{dt} = \mp \frac{qB}{m}v_x;$ $\frac{d v_z}{dt} = 0$

Last one is trivial:

\[v_z = v_\parallel\]

The other two in matrix form:

Where $\omega_c = qB/m$ is the (unsigned) gyrofrequency

Homogeneous ODE with solution:

\[\varphi = \mp \omega_c t + \varphi_0; \quad v_x = \pm v_\perp \sin\varphi; \quad v_y = \mp v_\perp \cos\varphi\]

The initial phase angle $\varphi_0$ is irrelevant here

Integrating again we get:

\[x = x_{gc} + \ell \cos \varphi; \quad y = y_{gc} + \ell \sin \varphi\]

$\ell = v_\perp/\omega_c = m v_\perp / (qB)$ is the (unsigned) gyroradius or Larmor radius

bg right:30% 100%

Constant and uniform $\bm B$ and $\bm E$ fields

Take $\bm B = B \bm 1z$ and $\bm E = E\parallel \bm 1z + E\perp\bm 1_y$:

The parallel part is trivial again

\[\frac{d v_z}{dt} = \pm \frac{q}{m}E_\parallel \quad \Rightarrow \quad v_z = v_{\parallel 0} \pm \frac{q}{m}E_\parallel t\]

The perpendicular part is a inhomogeneous ODE:

\[\frac{d }{dt} \left[ \begin{array}{c} v_x \\ v_y \\ \end{array} \right] = \pm\omega_c \left[ \begin{array}{cc} 0 & 1 \\ -1 & 0 \\ \end{array} \right] \cdot \left[ \begin{array}{c} v_x \\ v_y \\ \end{array} \right] \pm \frac{q}{m} \left[ \begin{array}{c} 0 \\ E_\perp \\ \end{array} \right]\] \[v_x = \frac{E_\perp}{B} \pm v_\perp \sin \varphi; \quad v_y = \mp v_\perp \cos \varphi\]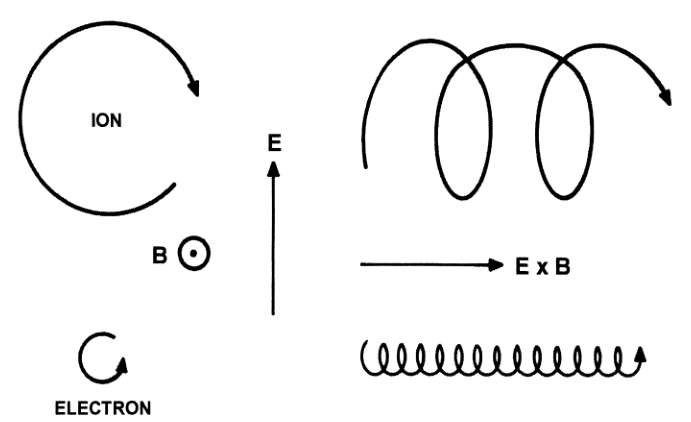

bg right:35% 100%

The motion is the sum of the following. In a local basis ${\bm 1b, \bm 1_r(\varphi), \bm 1\varphi(\varphi)}$:

A fast gyromotion about the gyrocenter with gyrofrequency $\omega_c$ and gyroradius $\ell$:

\[\bm v_c = \mp v_\perp \bm 1_\varphi\]

A slow drift, known as the ExB drift:
- The magnitude is $E_\perp/B$
- The ExB drift is independent of charge sign, $q$, $m$

\[\bm v_d = \frac{\bm E\times \bm B}{B^2}\]

An accelerated parallel motion, according to the $E_\parallel$ field:

\[\bm v_\parallel = \left[v_{\parallel 0} \pm \frac{q}{m}E_\parallel t\right]\bm 1_b\]

By the way: the ExB drift can also be understood transforming into a moving frame.

Define a frame $S^\prime$ that displaces with velocity $\bm v_d$ with respect to the original one $S$
In this frame the new $\bm E^\prime$ and $\bm B^\prime$ fields are as follows (non-relativistic limit):

\[\bm E^\prime = \bm E + \bm v_d \times \bm B = E_\parallel \bm 1_b; \quad \bm B^\prime = \bm B\]

This means that in $S^\prime$ we have $E_\perp^\prime = 0$, i.e. the gyromotion-only case

Final solution in constant, uniform fields

Using the local vector basis ${\bm 1b, \bm 1_r(\varphi), \bm 1\varphi(\varphi)}$:

\[\bm v = \bm v_d \mp v_{\perp 0} \bm 1_\varphi + v_{\parallel 0} \bm 1_b; \quad \varphi = \mp\omega_c t;\]

An extra force

Just like the $\pm q\bm E$ force gives rise to the ExB drift, an extra constant force $\bm F$ gives rise to a similar drift:

\[m\frac{d \bm v}{dt} = \pm q\bm v \times \bm B + \bm F \quad\Rightarrow\quad \bm v_d = \pm \frac{\bm F\times \bm B}{qB^2}\]

In this case, ions and electrons have opposite drift directions and a net current develops