Notes on single particle motion II
Variable fields
We will consider only cases with:
\[\ell \ll L; \quad v_\parallel / L \ll \omega_c; \quad |\partial \bm E/\partial t|/E \ll \omega_c; \quad |\partial \bm B/\partial t|/B \ll \omega_c\]where $L$ is the gradient length of changes in $\bm E$ and $\bm B$ ($L\sim E/|\nabla \bm E|\sim B/|\nabla \bm B|$). This ensures that the particle does not “see” large changes in $\bm E$, $\bm B$ within an orbit.
We introduce the small parameter $\varepsilon = \ell / L$ and rewrite $m/q \to \varepsilon \hat m/\hat q$, where $\hat m,\hat q$ are arbitrary normalization constants:
\[\varepsilon\frac{d \bm v}{dt} = \pm \frac{\hat q}{\hat m}(\bm E + \bm v \times \bm B); \quad \frac{d \bm r}{d t} = \bm v\]- We will study the limit $\varepsilon \to 0^+$ and drop the hat symbols for simplicity
Two-scale averaging method
There are two distinct timescales in the problem: $\tau_c = 1/\omega_c$ for the fast changes of the gyrophase $\varphi$, and $\tau$ for the slow changes of the position of the gyrocenter:
\[\tau_c \ll \tau \quad\Rightarrow\quad \frac{\tau_c}{\tau} \sim \varepsilon \ll 1\]- While the gyrophase is a function of time, $\varphi = \varphi(t)$, we will write all variables as functions of $t$ and $\varphi$ as if they were two independent variables:
- We will compute derivatives as: $\dfrac{d \bm r}{dt} = \dfrac{\partial \bm r}{\partial t} + \dot\varphi \dfrac{\partial \bm r}{\partial \varphi}$, with $\dot\varphi \approx \omega_c = O(1/\varepsilon)$
Next, we express our solution in the following form:
\[\bm r(t,\varphi) = \bm R(t) + \varepsilon \bm \rho(t,\varphi); \quad \bm v(t,\varphi) = \bm U(t)+ \bm u(t,\varphi)\]- $\bm R$ and $\bm U = \bm U_\perp + U_\parallel \bm 1_b$ describe the gyrocenter, with $\bm U = d\bm R/dt$
- $\bm \rho,\bm u$ represent the fast gyromotion:
- They are perpendicular to $\bm B(\bm R,t)$, i.e., $\bm \rho \cdot \bm 1_b =0$, $\bm u \cdot \bm 1_b =0$
- They are $2\pi$-periodic in $\varphi$ for fixed $t$
- They have zero $\varphi$-average:
The vector basis ${\bm 1b, \bm 1_r, \bm 1\varphi}$ is defined at $(\bm R,t)$.
Finally, we expand:
\[\bm R = \bm R_0 +\varepsilon\bm R_1 +\varepsilon^2\bm R_2 + \ldots \\ \bm U = \bm U_0 +\varepsilon\bm U_1 +\varepsilon^2\bm U_2 + \ldots \\ \bm \rho = \bm \rho_0 +\varepsilon\bm \rho_1 +\varepsilon^2\bm \rho_2 + \ldots \\ \bm u = \bm u_0 +\varepsilon\bm u_1 +\varepsilon^2\bm u_2 + \ldots\]The gyrophase evolves as:
\[\frac{d \varphi}{dt} = \frac{1}{\varepsilon}\Omega_{-1} + \Omega_0 + \varepsilon \Omega_1 + \ldots\]Magnetic field gradient:
Consider $\bm B (\bm R,t) = B_0 \bm 1_z$. The gradient of $\bm B$ has different terms:
\[\nabla \bm B = \left[ \begin{array}{cc|c} \partial B_x/\partial x & \partial B_y/\partial x & \partial B_z/\partial x \\ \partial B_x/\partial y & \partial B_y/\partial y & \partial B_z/\partial y \\ \hline \partial B_x/\partial z & \partial B_y/\partial z & \partial B_z/\partial z \\ \end{array} \right]\]- Diagonal terms are the divergence terms. Observe that always $\nabla \cdot \bm B = 0$
- The variation of $B_z$ with $x$ and $y$ are the gradient terms
- Variations of $B_x$, $B_y$ with $z$ are the curvature terms
- Terms $\partial B_x/\partial y$ and $\partial B_y/\partial x$ are shear terms
We write:
\[\bm B(\bm r,t)\simeq \bm B(\bm R,t) + \varepsilon(\bm \rho\cdot \nabla) \bm B (\bm R,t) + \ldots \\ \bm E(\bm r,t)\simeq \bm E(\bm R,t) + \varepsilon(\bm \rho\cdot \nabla) \bm E (\bm R,t) + \ldots\]and expand the magnetic force as:
\[\pm q\bm v \times \bm B = \pm q\bm v \times \bm B(\bm R,t) \pm \varepsilon q\bm v \times (\bm \rho\cdot\nabla)\bm B(\bm R,t)\]- The second term on the RHS can be thought of as a small “extra force” $\bm F$
Furthermore, we require that $E_\parallel$ be small:
\[\bm E(\bm R,t) = \bm E_\perp(\bm R,t) + \varepsilon E_\parallel(\bm R,t)\bm 1_b\]Leading order solution
To order $O(1/\varepsilon)$, the equation of motion reads:
\[\Omega_{-1}\frac{d \bm u_0}{d\varphi} \mp \frac{q}{m}\bm u_0 \times \bm B(\bm R,t) = \pm\frac{q}{m}\bm E_\perp(\bm R,t) \pm \frac{q}{m}\bm U_{\perp 0} \times \bm B(\bm R,t)\]Averaging in $\varphi$:
\[\bm 0 = \bm E_\perp(\bm R,t) + \bm U_{\perp 0} \times \bm B(\bm R,t)\]This yields
\[\bm U_{\perp 0} = \frac{\bm E_\perp(\bm R,t)\times \bm B(\bm R,t)}{B^2(\bm R,t)}\]Subtracting this from the equation:
\[\Omega_{-1}\frac{d \bm u_0}{d\varphi} \mp \frac{q}{m}\bm u_0 \times \bm B(\bm R,t) = \bm 0; \quad \Omega_{-1}\frac{d \bm \rho_0}{d \varphi} = \bm u_0\]In the local cylindrical vector basis, integrating and imposing periodicity in $\varphi$:
\[\bm u_0 = \mp u_{\perp 0} \bm 1_\varphi; \quad \Omega_{-1} = \mp \frac{qB(\bm R,t)}{m} = \mp\omega_c(\bm R,t); \quad \bm \rho_0 = \ell_0 \bm 1_r\]Thus, we recover the solution we already had for uniform, constant fields
Guiding center drifts
To order $O(1)$ the equation reads:
\[\Omega_{-1}\frac{\partial \bm u_1}{\partial \varphi} \mp \frac{q}{m}\bm u_1 \times \bm B(\bm R,t) + \frac{d \bm U_0}{dt} + \frac{\partial \bm u_0}{\partial t} + \Omega_{0}\frac{\partial \bm u_0}{\partial \varphi} \\ = \pm \frac{q}{m}E_\parallel(\bm R,t)\bm 1_b \pm \frac{q}{m}(\bm\rho_0\cdot\nabla)\bm E(\bm R,t) \pm \frac{q}{m}\bm U_{1\perp} \times \bm B(\bm R,t) \\ \pm \frac{q}{m}\bm U_{\perp 0} \times (\bm\rho_0\cdot\nabla)\bm B(\bm R,t) \pm \frac{q}{m}\bm u_0 \times (\bm\rho_0\cdot\nabla)\bm B(\bm R,t)\]Averaging in $\varphi$ eliminates most of the terms:
\[\frac{d \bm U_0}{dt} = \pm \frac{q}{m}E_\parallel(\bm R,t)\bm 1_b \pm \frac{q}{m}\bm U_{1\perp} \times \bm B(\bm R,t) \pm \frac{q}{m}\left<\bm u_0 \times (\bm\rho_0\cdot\nabla)\bm B(\bm R,t)\right>\]\[\pm \frac{q}{m}\left<\bm u_0 \times (\bm\rho_0\cdot\nabla)\bm B(\bm R,t)\right> = - \frac{q}{m} u_{\perp 0} \ell_0\left<\bm 1_\varphi \times (\bm 1_r\cdot\nabla)\bm B(\bm R,t)\right> \\ = \frac{q}{m} u_{\perp 0} \ell_0 \frac{1}{2\pi} \oint d\varphi \left[ \bm 1_b (\bm 1_r\cdot\nabla)\bm B(\bm R,t) \cdot \bm 1_r - \bm 1_r (\bm 1_r\cdot\nabla)\bm B(\bm R,t) \cdot \bm 1_b \right]\]
To work out this expression use a local Cartesian vector basis ${\bm 1_x,\bm 1_y, \bm 1_z}$, with \(\bm 1_r = \cos\varphi\bm 1_x + \sin\varphi\bm 1_y; \quad \bm 1_b = \bm 1_z\)
and use:
\[\nabla\cdot\bm B = \frac{\partial B_x}{\partial x} + \frac{\partial B_y}{\partial y} + \frac{\partial B_z}{\partial z} = 0\]After integrating, and noting that $\bm B(\bm R,t) = B_z(\bm R,t) \bm 1_z = B(\bm R,t) \bm 1_z$:
\[\pm \frac{q}{m}\left<\bm u_0 \times (\bm\rho_0\cdot\nabla)\bm B(\bm R,t)\right> = - \frac{q}{m} u_{\perp 0} \ell_0 \frac{1}{2} \nabla B(\bm R,t) = - \frac{u_{\perp 0}^2}{2B(\bm R,t)} \nabla B(\bm R,t)\]Introducing the (unsigned) magnetic moment at order $O(1)$:
\[\mu_0(\bm R,t) = \frac{m u_{\perp 0}^ 2}{2B(\bm R,t)}\]Now, we can rewrite the averaged equation as
\[m\frac{d \bm U_0}{dt} = \pm q E_\parallel(\bm R,t)\bm 1_b \pm q\bm U_{1\perp} \times \bm B(\bm R,t) -\mu_0(\bm R,t)\nabla B(\bm R,t)\]The parallel projection of this equation gives $U_{\parallel 0}$:
\[m\frac{d U_{\parallel 0}}{dt} = \pm q E_\parallel(\bm R,t) -\mu_0(\bm R,t)(\bm 1_b\cdot\nabla) B(\bm R,t) - m\bm 1_b \cdot\frac{d \bm U_{\perp 0}}{dt}\]Dropping the $(\bm R,t)$ dependency for the sake of notation:
\[m\frac{d U_{\parallel 0}}{dt} = \pm q E_\parallel -\mu_0(\bm 1_b\cdot\nabla) B - m\bm 1_b \cdot\frac{d \bm U_{\perp 0}}{dt}\]- The second term in the RHS is the magnetic mirror force
- It pushes particles in the direction of decreasing $B$ regardless of their sign
The perpendicular projection gives:
\[\bm U_{1\perp} = \pm \frac{\bm 1_b}{\omega_c(\bm R,t)} \times \left[ \frac{d \bm U_0}{dt} +\mu_0(\bm R,t)\nabla B(\bm R,t) \right]\]Dropping the $(\bm R,t)$ dependency for the sake of notation:
\[\bm U_{1\perp} = \pm \frac{\bm 1_b}{\omega_c} \times \left[ \frac{d \bm U_0}{dt} +\frac{\mu_0}{m}\nabla B \right]\]- The first term is known as the inertial drift
- The second term is the magnetic drift
Magnetic drift
\[\pm \frac{\mu_0}{m\omega_c} \bm 1_b \times \nabla B\]- It displaces the gyrocenter at right angles with $\partial B/\partial \bm 1_\perp$
- The effect is the opposite for positive and negative particles
- It depends on $m$ and on $u_{\perp 0}$ through $\mu_0$
Inertial drift
We split it in two parts. The derivative of $U_{\parallel 0}\bm 1_b$ gives:
\[\pm \frac{\bm 1_b}{\omega_c} \times \frac{d \bm U_{\parallel 0} \bm 1_b}{dt} = \pm \frac{U_{\parallel 0}}{\omega_c} \bm 1_b \times \frac{d \bm 1_b}{dt} \\ = \pm \frac{U_{\parallel 0}}{\omega_c} \bm 1_b \times \left[ \frac{\partial\bm 1_b}{\partial t} + (\bm U_{\perp 0} \cdot \nabla) \bm 1_b + U_{\parallel 0} (\bm 1_b \cdot \nabla) \bm 1_b \right]\]Using the curvature vector $\bm \kappa = (\bm 1_b \cdot \nabla) \bm 1_b$, the last part is the curvature drift:
\[\pm \frac{U_{\parallel 0}^2}{\omega_c} \bm 1_b \times \bm \kappa\]- It displaces the gyrocenter at right angles with $\bm \kappa$
- The effect is the opposite for positive and negative particles
- It depends on $m$ and on $U_{\parallel 0}^2$
The derivative of $\bm U_{\perp 0}$ gives:
\[\pm \frac{\bm 1_b}{\omega_c} \times \frac{d \bm U_{\perp 0}}{dt}\]- This is known as the polarization drift
- The effect is the opposite for positive and negative particles
Conservation of $\mu_0$ to $O(1)$
The equation of the $\varphi$-averaged kinetic energy of the particle reads:
\[\frac{m}{2} \frac{d}{dt} (u_{\perp 0}^2 + U_0^2) = \pm q U_{\parallel 0}E_\parallel \pm q \bm U_{\perp 1}\cdot \bm E_\perp \pm q \left<(\bm \rho_0\cdot \nabla)\bm E \cdot \bm u_0 \right>\]But:
\[m\bm U_0\cdot\frac{d \bm U_0}{dt} = \pm q U_{\parallel 0}E_\parallel \pm q\bm U_{\perp 0}\cdot (\bm U_{1\perp} \times \bm B) -\mu_0\bm U_0\cdot\nabla B\]And:
\[U_{\perp 0} = \frac{\bm E_\perp\times\bm B}{B^2} \quad\Rightarrow\quad \pm q\bm U_{\perp 0}\cdot (\bm U_{1\perp} \times \bm B)= \pm q \bm U_{\perp 1}\cdot \bm E_\perp\]Additionally:
\[\pm q \left<(\bm \rho_0\cdot \nabla)\bm E \cdot \bm u_0 \right> = \frac{m u_{\perp 0}^2}{2\pi B}\oint d\varphi (\bm 1_r \cdot \nabla)\bm E \cdot \bm 1_\varphi = - \mu_0 \bm 1_b \cdot \nabla \times \bm E = \mu_0 \frac{\partial B}{\partial t}\]Therefore:
\[\frac{m}{2} \frac{d}{dt} u_{\perp 0}^2 - \mu_0 \frac{\partial B}{\partial t} -\mu_0 \bm U_0\cdot \nabla B = 0\]Since $\mu_0 = u_{\perp 0}^2/(2B)$ and $dB/dt = \partial B/\partial t + \bm U_0 \cdot \nabla B$ in the averaged equation:
\[\frac{d}{dt} \mu_0 = 0\]- $\mu_0$ is conserved to lowest order and is therefore an adiabatic invariant
See HAZE18 p 29 to learn more about Poincaré invariants and Adiabatic invariants
Magnetic mirror
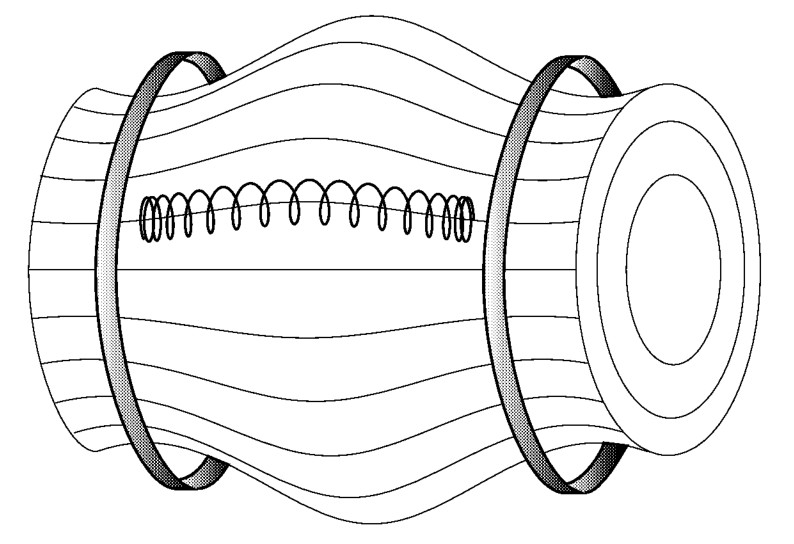
In stationary fields,
\[H = \frac{1}{2} mv_\parallel^2 + \mu B = \text{const}\] \[\mu = \frac{mv_\perp^2}{2B} = \text{const}\]- Particles trade parallel to perpendicular kinetic energy as they move toward a region of maximum $B$
- If $B_{max}$ at the maximum, only particles with $v_\perp^2/v^2 < B/B_{max}$ can escape. This defines a loss cone in phase space
Further reading
- I have followed mainly HAZE18 (with adaptations)
- BITT04 gives an ad-hoc derivation for each drift, but easier to understand
- litt83 is a beautiful derivation based on Hamiltonian dynamics—maybe a topic for another time