Notes on plasma sheaths

I follow Bittencourt’s and Chabert’s books

Why sheaths form

• Plasma has a large number of massive positive ions and light negative electrons
• The thermal velocity of each is $v_j\sim\sqrt{T_j/m_j}$, $j=i,e$
• Even when $T_i\sim T_e$, $v_e \gg v_i$. In most cases, $T_i \ll T_e$, so this is even more so.
• Hence, electrons are more mobile than ions, and more electrons than ions would be collected by the walls in a fixed amount of time.
• Unless the wall cannot continuously collect charge current, this situation cannot last long: the wall will acquire negative charge in a short transient
• Thereafter, the wall is at a lower potential than the bulk plasma: this reflects most of the electrons back and allows having $j_i=j_e$ at the wall
• This is the so-called floating potential
• The potential structure happens in a thin layer near the wall, of characteristic length $\lambda_D = \sqrt{\varepsilon_0 T_e/(ne^2)}$: a sheath

Assumptions

The simplest sheath model assumes:

• Steady-state, collisionless, quasineutral, uniform bulk plasma made of cold ions at rest and Maxwellian electrons
• An infinite flat wall with no emission
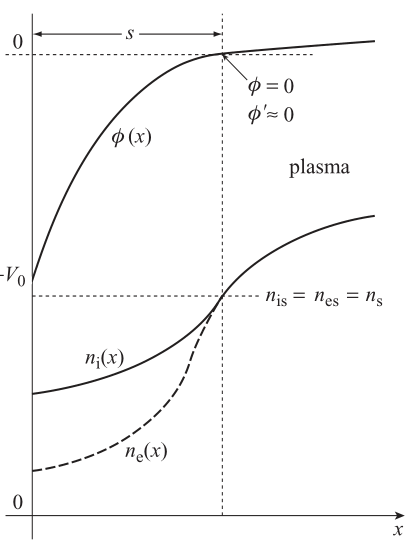
• We take the origin $x=0$ at the wall, where $\phi=\phi_w$
• At some distance $x=s$, $\phi=0$, $d\phi/dx\simeq 0$, $u_i=u_{is}$, and $n_e=n_i=n_s$.

Basic equations and sheath solution

Neglecting electron inertia, their momentum equation reads \(0 = -\frac{1}{n_e}\frac{d (n_eT_e)}{d x} + e\frac{d\phi}{dx}\) If most electrons are repelled by the sheath, to a good approximation they satisfy the Boltzmann relation with constant $T_e$: \(n_e(x) = n_s \exp\left[ \frac{e \phi(x)}{T_e}\right]\)

Cold ions momentum equation can be integrated into the conservation of ion mechanical energy: \(m_i u_i \frac{du_i}{dx} = - e\frac{d\phi}{dx} \quad\Rightarrow\quad \frac{1}{2}m_i u^2_i(x) + e\phi(x) = \frac{1}{2}m_i u^2_s\)

The 1D continuity equation of ions states simply \(n_i(x) = \frac{n_su_{is}}{u_i(x)} =n_s\left[1-\frac{2e\phi(x)}{m_iu_{is}^2}\right]^{-1/2}\)

Sheath equation

Poisson’s equation for $\phi$ reads: \(\frac{d^2\phi}{dx^2} = \frac{e}{\varepsilon_0} [n_e(x)-n_i(x)]\) Substituting, we obtain the sheath equation: \(\frac{d^2\phi}{dx^2} = \frac{en_s}{\varepsilon_0} \left\{\exp\left[ \frac{e \phi(x)}{T_e}\right]-\left[1-\frac{2e\phi(x)}{m_iu_{is}^2}\right]^{-1/2}\right\}\)

This is a nonlinear equation that must be solved with the condition $j_i = j_e$ at $x= 0$.

Observe that $u_{is}$ is still unknown.

We can find a condition on $u_{is}$ if we linearize the equation about $x=s$, \(\frac{d^2\phi}{dx^2} = \frac{en_s}{\varepsilon_0} \left\{\left[1 + \frac{e \phi}{T_e}\right]-\left[1+\frac{e\phi}{m_iu_{is}^2}\right]\right\} \\ = \frac{e^2n_s}{\varepsilon_0} \left\{\frac{1}{T_e}-\frac{1}{m_iu_{is}^2}\right\}\phi = \frac{1}{\lambda_D^2} \left\{1-\frac{T_e}{m_iu_{is}^2}\right\}\phi\)

• If $m_i u_{is}^2 < T_e$, the curly bracket is negative and this equation has oscillatory solutions (imaginary eigenvalues)
• If $m_i u_{is}^2 > T_e$, it has monotonic exponential solutions (real eigenvalues).

Bohm’s criterion states that $u_{is} \geq \sqrt{T_e/m_i}$ (Bohm’s velocity) at the sheath edge. I.e., ions must arrive at the sheath edge with sonic velocity.

• There is a pre-sheath region matching the sheath with the bulk, in which ions are gradually accelerated to meet this condition.

Observe that if $n_i=n_e=n_s$, $u_i=u_{is}=\sqrt{T_e/m_i}$ at the sheath edge $x=s$, the density $n_0$ far into the plasma is higher: \(m_i u_i \frac{du_i}{dx} = - T_e\frac{d \ln n}{d x} \quad\Rightarrow\quad \frac{1}{2} T_e = -T_e \ln n_s + T_e \ln n_0\)

• The density is not constant in the presheath

Sheath potential

• The ion flux $\Gamma_i = n_i(x)u_i(x)= n_su_{is}$ is constant across the sheath. Moreover, it is independent of $\phi_w$.
• The one-sided kinetic flux of electrons (assuming a Maxwellian population) is \(\Gamma_e = n_e \sqrt{\frac{T_e}{2\pi m_e}}\)
• Imposing the condition $\Gamma_e-\Gamma_i = 0$ at $x=0$ allows finding the potential fall in the sheath \(n_s \exp\left(\frac{e\phi_w}{T_e}\right) \sqrt{\frac{T_e}{2\pi m_e}} - n_s\sqrt{\frac{T_e}{m_i}} = 0 \quad\Rightarrow\quad \phi_w = - \frac{T_e}{2e}\ln \left(\frac{m_i}{2\pi m_e}\right)\)
• Any other potential (e.g. externally imposed) will result in $\Gamma_e \neq \Gamma_i$, and therefore current collection.

More complex models

• A conducting wall may accept a nonzero charge current, e.g. if we bias it externally at a different voltage than the floating potential. The current-voltage response is called the I-V characteristic, and is essential for Langmuir probe analysis.
• If emission from the wall takes place (e.g. secondary electrons emitted by ion or electron impact), an extra, near-monoenergetic electron population is present in Poisson’s equation. The potential may even become non-monotonic in the sheath (emission saturation).
• Ion temperature modifies the obtained results, especially the Bohm condition.
• Electrons may be non-Maxwellian, requiring a fully-kinetic model to solve the sheath.

RF sheaths

Imagine now that we have the set up of the figure, and we bias a section of the wall with a sinusoidal AC voltage at angular frequency $\omega$. The capacitor stills prevent any DC current to the wall, but within each AC cycle instantaneous current may be collected.

Alternatively, the plasma potential may vary at a frequency $\omega$, giving rise to similar effects.

Read more: Chabert’s chapter 4

Plasma frequency of ions and electrons

The characteristic times in which a typical ion or traverses a Debye length are \(\tau_i = \frac{\lambda_D}{\sqrt{T_e/m_i}} = \omega_{pi}^{-1}\) \(\tau_e = \frac{\lambda_D}{\sqrt{T_e/m_e}} = \omega_{pe}^{-1}\) Here, $\omega_{pi}$, $\omega_{pe}$ are the ion and electron plasma frequency, respectively.

• For $n = 10^{18}$ m$^{-3}$, $T_e = 5$ eV, Xenon plasma: $\omega_{pi}= 0.1$ and $\omega_{pe} = 56$ GHz
• Observe that $\omega_{pi}\ll \omega_{pe}$.

1. If $\omega \ll \omega_{pi}$, the AC frequency is so slow that ions and electrons do not see any major changes during their passage through the sheath. The solution is essentially a collection of quasi-static solutions, based on the stationary I-V characteristic.
2. If $\omega_{pi} \sim \omega \ll \omega_{pe}$, the slower ions see the change while in the sheath, but the solution of the faster electrons is essentially quasi-static. Ions gain a different amount of energy depending at which instant they enter the sheath, complicating their dynamics
3. If $\omega_{pi} \ll \omega \ll \omega_{pe}$, oscillations are too fast to have an impact on the ions, so they barely disturb them. Electrons are able to redestribute quickly in response to $\omega$.
4. If $\omega_{pi} \ll \omega \sim \omega_{pe}$, The effect on electrons is large. Their dynamics are complex.
5. If $\omega_{pe} \ll \omega$, oscillations are too fast for either ions or electrons to follow them. In essence, we have the DC solution again.

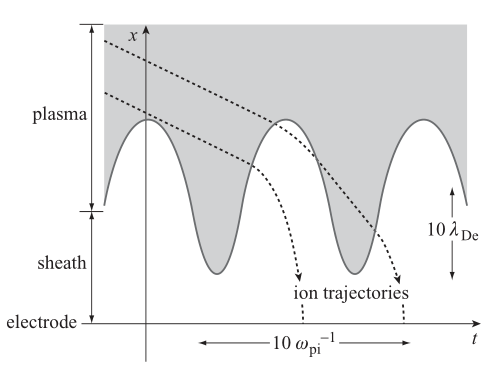
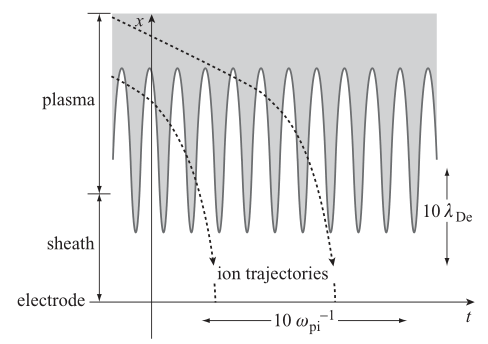
When the potential difference increases, so does the sheath width.These figures exemplify the motion of ions in the varying sheath.The greatest effect on ion motion happens when their transit time in the sheath is similar to the RF time.

Regardless, the average ion flux continues to be \(\left<\Gamma_i\right>= n_s\sqrt{\frac{T_e}{m_i}}\)

Electron response

As long as $\omega \ll \omega_{pe}$, electron response to the varying potential is instantaneous. The electron current collected by the wall is: \(n_s \exp\left(\frac{e\phi_w(t)}{T_e}\right) \sqrt{\frac{T_e}{2\pi m_e}}\)

Electron response is exponential:

• An increase of $\phi_w$ with respect to the DC floating potential (i.e., if the potential difference with the wall decreases) means a huge avalanche of electrons
• When $\phi_w$ becomes more negative, the small electron current becomes even smaller.

RF floating potential

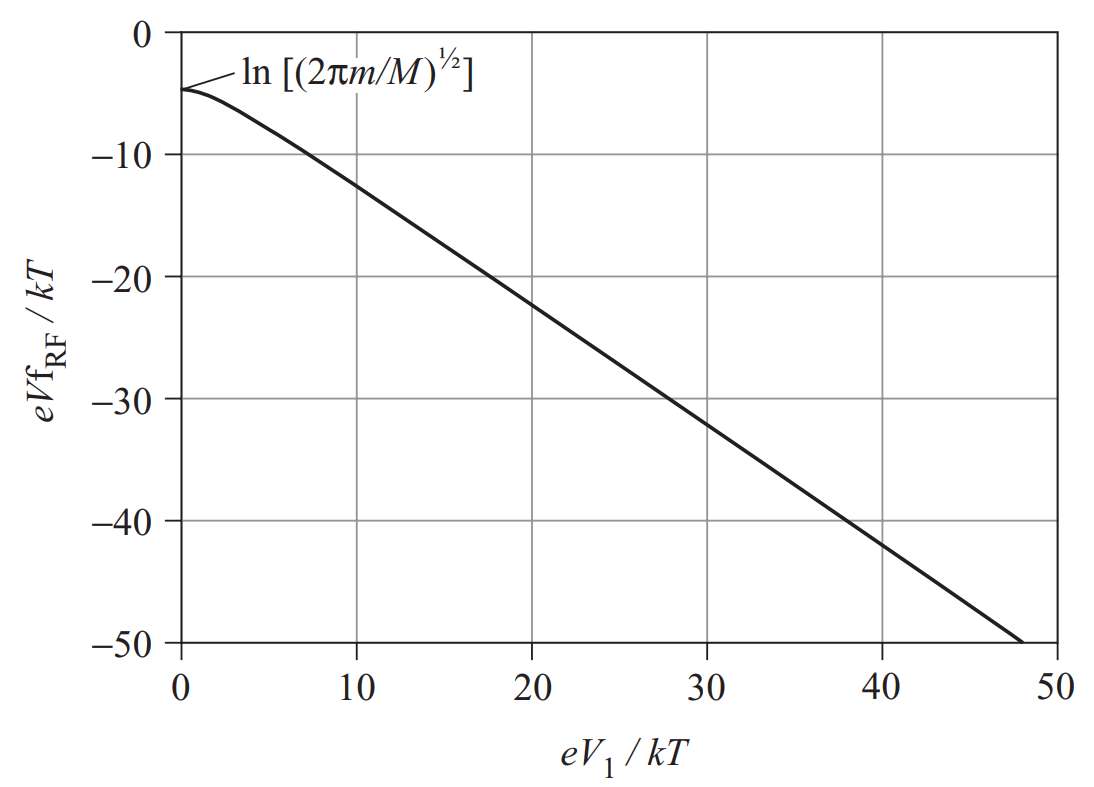
The floating potential is different in this case due to the rectifying effect of electron motion. Averaging over an RF period:

Integrating we find that the floating potential becomes more negative, due to the so-called RF self bias: \(\phi_w = \frac{T_e}{2e}\left[ -\ln \left(\frac{m_i}{2\pi m_e}\right) -\ln \left(\mathrm{I}_0\left(\frac{e\phi_1}{T_e}\right)\right) \right]\)

• Here, $\mathrm{I}_0$ is the modified Bessel function of zeroth order, with $\mathrm{I}_0(0)=1$ and $\mathrm{I}_0(x)>1$ for $x>0$.